Néha betalálunk

Lassan két hónapja záporoznak az ubrokaszezonos sörmeccs-kommentfogók, húspiaci mérlegcikkek és Lackó-féle kérek-még mesedélutánok. Most mindenki kitörő örömére elvesszük a zsugát tőletek, és kemény stat-alapozós napot tartunk. Véletlenül sem szeretnék senkit lebeszélni róla, hogy legörgessen a végére, de ez nem csak Máté-Glen-féle gyereknapi móka lesz. Hanem az oly sokszor vita tárgyát képező ExpGoal kivesézése. Mi ez, hogy lehet egy ilyet jól felépíteni, miért jók a mai modellek, és az is, hogy miért szarok. Kurva elméleti írás jön, akit nem riaszt el, annak virtuális nyelves csókot küldd a Jacuzzi bármely örömlánya.

xG, xGoal, ExGoal, ExpGoal, ExpG, Expected Goal, csilliónyi angol rövidítése van, ezért én most következetesen a magyar várható gólszámot fogom használni. (Meg a legrövidebb xG-t.) Teszem ezt nulladik lépésben azért, mert már a szóösszetétel első tagjánál meg kéne pihennünk egy pillanatra. Várható.

A várható érték minden bizonnyal a statisztika legfontosabb alapfogalma. Szerintem a legjobb intuitív definíciója a következő: egy adott kísérlet ismételgetéséből adódó eredmények hosszú távú átlaga. Minden szava nagyon fontos:

• egy adott kísérlet: ezek a kísérletek bizonyos tulajdonságaikban megegyeznek – a dobókocka mindig ugyanolyan, pikkből mindig 13 van a pakliban, …
• hosszú távú: csak hosszú távon fog érvényesülni, hogy a várható érték jó becslése lesz _valaminek. Senki nem használ statisztikát egy-két meccses jósgömbözésre. Vagy aki igen, azt csapjátok arcon.
• átlaga: nem feltétlen van ennek a számnak bármi értelme. Pl. kockadobásnál a várható érték 3,5. Jelent ez bármit? Az ég világon semmit. De ha tudjuk pl., hogy a mögöttes eloszlás haranggörbe (haladóknak: normális eloszlás), akkor az azt jelenti, hogy ezen érték köré bizony nagy valószínűséggel fog esni a kísérlet kimenetele (lásd ábra), szóval ha erre tippelünk, a legkisebb rosszat választjuk előzetesen. Abba most bele nem megyek, miért, de a természetben kb. minden érdekes dolog ilyen haranggörbe lesz. A dolgozatok eloszlása, a napraforgótáblára eső szotyik száma, vagy Sterling következő gyerekének várható magassága. Nem vicc. És a lőtt gólok száma is egy meccsen.

Szóval az a nagyon király dolog, hogy ha veszünk egy sokmeccses mintát (PL-szezon) és ott egy csapat lőtt góljainak számát, akkor hosszú távon átlagosan a fenti ábra 0 pontjának környékén fog ez elhelyezkedni jó nagy valószínűséggel. (A százalékokat is le lehet olvasgatni, általában 95%-ot szokás megadni, ami ugye +-1,96-szor a szórás, ha az mond valamit.) A 0 persze tolódik, mondjuk egy Pool esetén egy jó évben 80-ra. A baj az, hogy gőzünk nincs, mi is pontosan ez a szám, meg hogy ez a fenti görbe mennyire púpos. Ennek megoldásáról szól a statisztika. Veszünk elég sok megfigyelést, és akkor már meg tudjuk becsülni ezt az átlagszámot, vagy más néven várható értéket.

Az xG a várható gólszám egy adott meccsen a kialakított helyzetek, stb. függvényében. Michael Caley alkotta a cuccost (vagyis ez vitás, lejjebb lesznek részletek), mindjárt bele is megyünk a mélyébe, előbb azonban a fenti definíciót pörgessük át rá:

• adott kísérlet: igen, lövés minden, az hogy sok tényező befolyásolja – majd látni fogjuk, hogy ezeket próbáljuk kiszűrni;
• hosszú távú: idegeimre mennek a kommentek, mikor kiragadnak egy példameccset, hogy na te oktondi faszfej statisztikus, 3-0 helyett 1-3 lett. Leül, egyes. Ha minden meccsen kijönne az átlag, vagyis a várható érték, akkor a fotelből néznénk végig, ahogy a következő 70 évben mindig 7. helyen végzünk. Hagyjál, erről szól a természet, az ember, a focista: van benne egy véletlen, és a statisztika ez csípi nyakon, de véletlenül sem próbálja meg kiiktatni a természet törvényét;
• átlag: igen, majd meglessük a modellt.

Amikor leültem, hogy átnyálazzam a netet a cuccos után, kb. annyit tudtam (gondoltam), hogy van Michael Caley, a téma istene az úttörő cikkével, és hogy mindenki azt használva készítget csinos ábrákat a meccsek után, hogy aztán jól összevesszen rajta a Fonat közössége. Na, hogy ez mennyire nincs így, és hogy Caley mennyire nem is isten ezzel a modellel, az következzék most.

Arra, hogy statisztikai alapon próbáljuk előrejelezni a gólszámot, már lehet, hogy Rush-ék idején is felmerült valakiben, de persze csak a big data korszakban kezdték el tényleg megvalósítani. A differentgame blog szereti magára vállalni, hogy 2012 októberében ők kezdték el. Hát lol, nézzetek rá az alábbi ábrára.

Területi alapon (igen, össz-vissz 3-féle van) készítettek statot a várható gólra és a várható értékre. Gyönyörű, csak egy ilyen haranggörbe annyira lapos (széles), hogy ez a bizonyos 95%-os terület az átlag környékén azt jelenti kb., hogy várhatón 2 gólt rúgunk, de ha majdnem tutit akarok mondani (95%-kal), akkor valahol -3 és 12 között lesz. Köszi.

Ezért kellett finomítani ezt az őskövületet, ami tényleg csak a megértést szolgálja. Szóval minél több faktor bevételével kéne csökkenteni ezt az intervallumot, hogy ha azt mondjuk, hogy 2.3 xG, akkor amögött olyasmi is ott legyen, hogy hosszú távon ez tényleg 2 és 2.6 között van mondjuk. Hogy lehet ezt mérni, hogy mennyire szór ez a becslés? Kétféleképpen:

1. simán megnézegetjük a mintaátlag szórását és felírjuk (sajnos ezt kb. sosem látjuk sehol, amin mindig fel is baszódom, de valszeg egy újságíró fontosabbnak tartja az egy érték + szép ábra kombót, amivel amúgy semmi baj, csak én elkezdem kiköpni a sörömet)
2. évvégi összesített csapatgólszámokon visszateszteljük, mennyire működött jól a modell – na ez már szokott lenni az igényesebben vázolt cikkekben, de elég kiábrándító a kép itt is.

Ezzel annyit szeretnék mondani, hogy persze, hogy a statisztika egy gonosz dolog, mert mindenki úgy hamisítja, ahogy jól esik. De csak azért lehet gonosz, mert van, aki ilyen tesztek nélkül el is hiszi. Pedig tesztek nélkül nem statisztika a statisztika. Főleg nem a mai, borzalmasan nagy adathalmazokra épülő modellalapú statozás. (mint az xG is)

Gyönyörű statisztika és egyben modell, de itt is hiányzik egy teszt. Pl. átlag 100 férfiból 100 nem látja meg a majmot, de ha 95%-os bizonyossággal akarok igazat mondani a kísérleteim alapján, akkor valahol 98 és 100 között van ez a szám.

Jöjjön végre ezek után ténylegesen az xG modell boncolása.

Szóval ott vagyunk, hogy van valami haranggörbénk, aminek egyrészt a közepét szeretnénk eltalálni, másrészt púposítani szeretnénk, hogy ez a 95%-os sáv nagyon szűk legyen. Erre egy megoldás van: kurva sok olyan változót veszünk, ami a lövés góllá avagy nem góllá válását befolyásolhatja. Amikor pedig azt mondjuk, hogy na, több ötletem már nincs, akkor tesztelgetjük, hogy mennyire nyúltunk bele a tutiba.

A differentgame-es arcok után 2013-ban a Statsbombon Constantinos Chappas állt elő egy fejlettebb verzióval. A petit probléme ezzel, hogy sehol nem tette közzé a módszertanát. Még PirateBay-en sem, pedig rákerestem. Szót sem érdemel így tovább. Annál inkább a már emlegetett Michael Caley. 2014-ben írta meg az úttörő cikkét. 7 darab változót hoz be a képbe (ami igazából sokkal több):

1. lövés helye: ideértve a távolságot és a szöget
2. lövés típusa: 5-félét különböztet meg (normál, fejes beadásból, fejes nem beadásból, beadásból lőtt nem fejes, csel utáni)
3. lövést megelőző passz típusa
4. a támadás sebessége
5. a támadás során hány hosszú átadás volt
6. megelőző cselek típusai
7. rögzített szituáció előzte-e meg.

Elég ígéretesnek tűnik ez így, azt hogy mit hogyan képletezett fel, már tényleg nem fejtem itt ki, mert így is túl hosszú vagyok. De a cikkben minden le van matekozva, abszolút könnyen emészthető.

Jó, hogyan szerepelt ez a modell a teszteken? Hát öcsém, itt bizony nagyon elkúrta Michael. Merthogy egyrészt csak a változók egyenkénti visszatesztelését nézte (ami már önmagában elégtelen), és ezt ráadásul úgy, hogy az egyes változóknál a csoportátlagokat véve illesztett függvényt és nézett illeszkedést. Példa:

Erre itt leírta, hogy 99% feletti R-négyzete van. (R-négyzet: a valós pontok illesztett egyenestől vett átlagos eltérések négyzetösszege osztva az átlagtól vett átlagos eltérések négyzetösszegével.) 1) Ez szerinted egyenes? Ugye hogy nem? Innentől R-négyzet badarság. 2) Ilyen 8-10 csoportra bontásnál persze, hogy szép illeszkedésed lesz, de ha megcsinálod a valós adatokra, mint egy amcsi cikk:

Mindjárt más a molekula. Ezt és még több hibát emel ki kritikai cikkében Michael Bertin. A csóka az egyik legnagyobb stat-modellezős közösségi oldalon szerkesztő, szóval ért hozzá. Ehhez képest ő is elbaszta, lol.

Egyrészt ő tovább fejleszti Caley modelljét (ha már ráér), és még beletette az alábbiakat is:

• hónap
• liga
• idegen vagy hazai meccs
• meccs aktuális állása a lövés pillanatában
• 1. vagy 2. félidő.

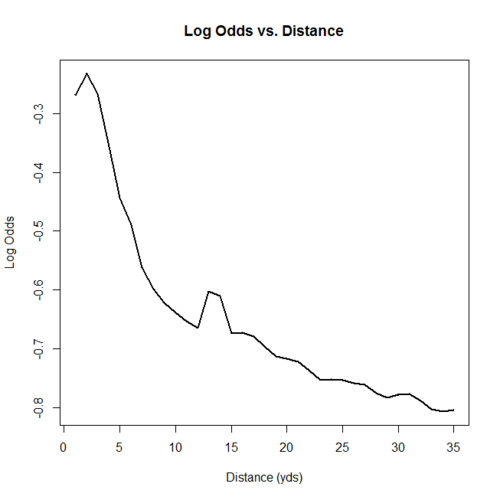
Mindegyik make sense. Na de ő is elérkezik a teszteléshez. A kurva jó ötlete, és ma már mindenki ezt használja, hogy a fentebb említett 2. típusú tesztre nem csak a gólszámon tesztel, hanem egyenként a lövéseken. Erre pedig logisztikus regressziót használ. Na ha a regresszió megvan (sok pöttyre illesztünk egy egyenest), akkor a logisztikus is: itt a sok pötty 0 és 1 lehet. Gól vagy nem gól. Erre egyenest illeszteni badarság, ezért egy ilyen S-görbe lesz a technika:

Ez tehát azért faszipántos, mert minden egyes megfigyelésre (lövésre) megnézzük, hogy a modellünk milyen valószínűséget tippelt a gólra, meg hogy konkrétan tényleg bement-e és erre nézegetünk teszteket. Na de a fenti S-görbe szerinted sem egyenes, ugye? Mert hogy ez az amúgy kurva okos ember miután lehordta a pékbe Caley R-négyzetét, most erre számolt egyet. És kapott 12.1%-ot, majd felbaszva magát 16.5-öt, miután hozzáadta a saját (fent említett) változóit. Aztán hagyta a pitlibe az egészet, és elvonult kutatni mást.

Miközben ezek az értékek – bár R-négyzet itt kurvára nem használható -, de nagyon is jók – főleg ha ránézünk a Caley- meg az amcsi-féle ábrákra, amik nincsenek is olyan messze egymástól, illetve az alábbi Statsbombos grafikonra, ami (minden bizonnyal) hasonló alapokon nyugvó modellen tesztelte vissza az eredményeket – de sajnos nem logisztikus regresszió felfogásban. Amúgy logisztikus regressziónál ilyesmi meg ilyen meg emilyen teszteket használunk. Több tucat cikket elolvastam a témában. Senkinél sem láttam ilyet…

Szóval elég savanyú a szőlő, mert a sehonnai átlag internetbetyárnak nem enged senki betekintést a modelljébe. Konkrét regressziós együtthatókat is ritkán látni, tesztértékeket meg aztán pláne nem. Nem olyan meglepő talán, hisz ezeket mindenki magának fejleszti, és védi a kincsét, mint anyamaci a bocsát.

Az sem véletlen, hogy irgalmatlan sokféle modell született már:

• itt egy amcsi elemzés konkrét regressziós számokkal
• 11tegen11 szokott sokszor eredményeket közölni meccs után (modellrészleteket ő sem publikált)
• Beez is kreált egy Poolos modellt TTT-n, hát ez inkább csak megmosolyogtató
• Caley szintén elkezdte bővítgetni a saját modelljét – a mai modellek elvileg már 30 feletti változószámmal dolgoznak, például a játékos fizetése is benne van. Azért ez piszok jónak néz ki, főleg, hogy már az elején elég jó modellje volt.

Nagyon pezseg tehát a téma. És kétség ne essék, piszok jó modellek léteznek ma már. Elég ránézni pl. erre az xG előrejelzésre. Persze, nem találja el teljesen, hisz nem az ideális világban élünk, de nagyon sok helyen közel jár az igazsághoz. A problémám minden ilyennel csak annyi, hogy black boxok. Látjuk a felszínüket, és hogy egész jól működnek, de konkrét modelleket és ezek korrektül visszaszámolt teljesítményét csak nagyon ritkán látni.

A lényeg viszont a fenti két cikkből lejött xG tekintetében: minél több lövésadatot veszünk, ezeknél minél több mutatót vizsgálunk, és bedobáljuk egy logisztikus regresszióba (amit majd a stat szoftver kiköp nekünk ezek alapján). Ebből becslünk egy, az adott meccsen leadott lövésekből várt gólszámot. Ennek az egy számnak így meccs után nem sok értelme van, de ha év végén visszanézünk, miért lőttünk sokat/keveset, akkor a regresszió együtthatóiba kell beleásnia magát a lelkes válaszkeresőnek. És rá is fog bukkanni, ha egy mai, szofisztikált modellel dolgozott.

_________________________________________________________________________
Disclaimer:
Akinek megfeküdte a gyomrát, abszolút megértem, és elnézést kérek a szenvedős nyári keddjéért. De ha egy ilyen alapozáson átesel, akkor jobban fogod bírni a meccsek utáni statáradatot, mint Emre Can az 50 meccses szezonunkat napi 3 edzéssel. Peace.